NCERT Class 12th Math Syllabus and All Details 2025-2026

The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society. Senior Secondary stage is a launching stage from where the students go either for higher academic education in Mathematics or for professional courses like Engineering, Physical and Biological science, Commerce or Computer Applications. The present revised syllabus has been designed in accordance with National Curriculum Framework 2005 and as per guidelines given in Focus Group on Teaching of Mathematics 2005 which is to meet the emerging needs of all categories of students. Motivating the topics from real life situations and other subject areas, greater emphasis has been laid on application of various concepts.

Objectives

The broad objectives of teaching Mathematics at senior school stage intend to help the students:

• to acquire knowledge and critical understanding, particularly by way of motivation and visualization, of basic concepts, terms, principles, symbols and mastery of underlying processes and skills.
• to feel the flow of reasons while proving a result or solving a problem.
• to apply the knowledge and skills acquired to solve problems and wherever possible, by more than one method.
• to develop positive attitude to think, analyze and articulate logically.
• to develop interest in the subject by participating in related competitions.
• to acquaint students with different aspects of Mathematics used in daily life.
• to develop an interest in students to study Mathematics as a discipline.
• to develop awareness of the need for national integration, protection of environment, observance of small family norms, removal of social barriers, elimination of gender biases.
• to develop reverence and respect towards great Mathematicians for their contributions to the field of Mathematics.

Three Hours                      Max Marks: 80

*No chapter/unit-wise weightage. Care to be taken to cover all the chapters.

Unit-I: Sets and Functions

1. Sets

Sets and their representations, Empty set, Finite and Infinite sets, Equal sets, Subsets, Subsets of a set of real numbers especially intervals (with notations). Universal set. Venn diagrams. Union and Intersection of sets. Difference of sets. Complement of a set. Properties of Complement.

2. Relations & Functions

Ordered pairs. Cartesian product of sets. Number of elements in the Cartesian product of two finite sets. Cartesian product of the set of reals with itself (up to R x R x R). Definition of relation, pictorial diagrams, domain, co-domain and range of a relation. Function as a special type of relation. Pictorial representation of a function, domain, co-domain and range of a function. Real valued functions, domain and range of these functions, constant, identity, polynomial, rational, modulus, signum, exponential, logarithmic and greatest integer functions, with their graphs. Sum, difference, product and quotients of functions.

3. Trigonometric Functions

Positive and negative angles. Measuring angles in radians and in degrees and conversion from one measure to another. Definition of trigonometric functions with the help of unit circle. Truth of the identity 𝑠𝑖𝑛2𝑥 + 𝑐𝑜𝑠2𝑥 = 1, for all x. Signs of trigonometric functions. Domain and range of trigonometric functions and their graphs. Expressing 𝑠𝑖𝑛 (𝑥 ± 𝑦) and 𝑐𝑜𝑠 (𝑥 ± 𝑦) in terms of 𝑠𝑖𝑛𝑥, 𝑠𝑖𝑛𝑦,𝑐𝑜𝑠𝑥 & 𝑐𝑜𝑠𝑦 and their simple applications. Deducing identities like the following:

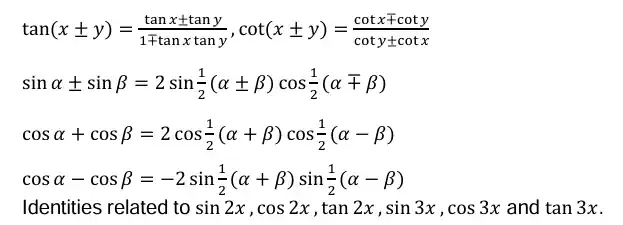
Identities related to sin2𝑥,cos2𝑥,tan2𝑥,sin3𝑥,cos3𝑥 and tan3𝑥.

Unit-II: Algebra

1. Complex Numbers and Quadratic Equations

Need for complex numbers, especially √−1, to be motivated by inability to solve some of the quadratic equations. Algebraic properties of complex numbers. Argand plane.

2. Linear Inequalities

Linear inequalities. Algebraic solutions of linear inequalities in one variable and their representation on the number line.

3. Permutations and Combinations

Fundamental principle of counting. Factorial n. (n!) Permutations and combinations, derivation of Formulae for n r P, n r C and their connections, simple applications.

4. Binomial Theorem

Historical perspective, statement and proof of the binomial theorem for positive integral indices. Pascal’s triangle, simple applications.

5. Sequence and Series

Sequence and Series. Arithmetic Mean (A.M.) Geometric Progression (G.P.), general term of a G.P., sum of n terms of a G.P., infinite G.P. and its sum, geometric mean (G.M.), relation between A.M. and G.M

Unit-III: Coordinate Geometry

1. Straight Lines

Brief recall of two-dimensional geometry from earlier classes. Slope of a line and angle between two lines. Various forms of equations of a line: parallel to axis, point -slope form, slope-intercept form, two-point form, intercept form. Distance of a point from a line.

2. Conic Sections

Sections of a cone: circles, ellipse, parabola, hyperbola, a point, a straight line and a pair of intersecting lines as a degenerated case of a conic section. Standard equations and simple properties of parabola, ellipse and hyperbola. Standard equation of a circle.

3. Introduction to Three-dimensional Geometry

Coordinate axes and coordinate planes in three dimensions. Coordinates of a point. Distance between two points.

Unit-IV: Calculus

1. Limits and Derivatives

Derivative introduced as rate of change both as that of distance function and geometrically. Intuitive idea of limit. Limits of polynomials and rational functions trigonometric, exponential and logarithmic functions. Definition of derivative relate it to scope of tangent of the curve, derivative of sum, difference, product and quotient of functions of polynomial and trigonometric functions.

Unit-V: Statistics and Probability

1. Statistics

Measures of Dispersion: Range, Mean deviation, variance and standard deviation of ungrouped/grouped data.

2. Probability

Events; occurrence of events, ‘not’, ‘and’ and ‘or’ events, exhaustive events, mutually exclusive events, Axiomatic (set theoretic) probability, connections with other theories of earlier classes. Probability of an event, probability of ‘not’, ‘and’ and ‘or’ events.