Find the Highest Common Factor (HCF) and the Lowest Common Multiple (LCM) of 510 and 92.

HCF Calculation

The HCF is the largest number that divides both 510 and 92 without a remainder. Using the prime factorization method:

• 510 = 2×3×5×17

• 92 = 22×23

The only common prime factor is 2, with the lowest power being 2121. Thus, the HCF is 2.

Alternatively,using the Euclidean algorithm:

• 510 ÷ 92 = 5 with remainder 50 (510 = 92 × 5 + 50)

• 92 ÷ 50 = 1 with remainder 42 (92 = 50 × 1 + 42)

• 50 ÷ 42 = 1 with remainder 8 (50 = 42 × 1 + 8)

• 42 ÷ 8 = 5 with remainder 2 (42 = 8 × 5 + 2)

• 8 ÷ 2 = 4 with remainder 0

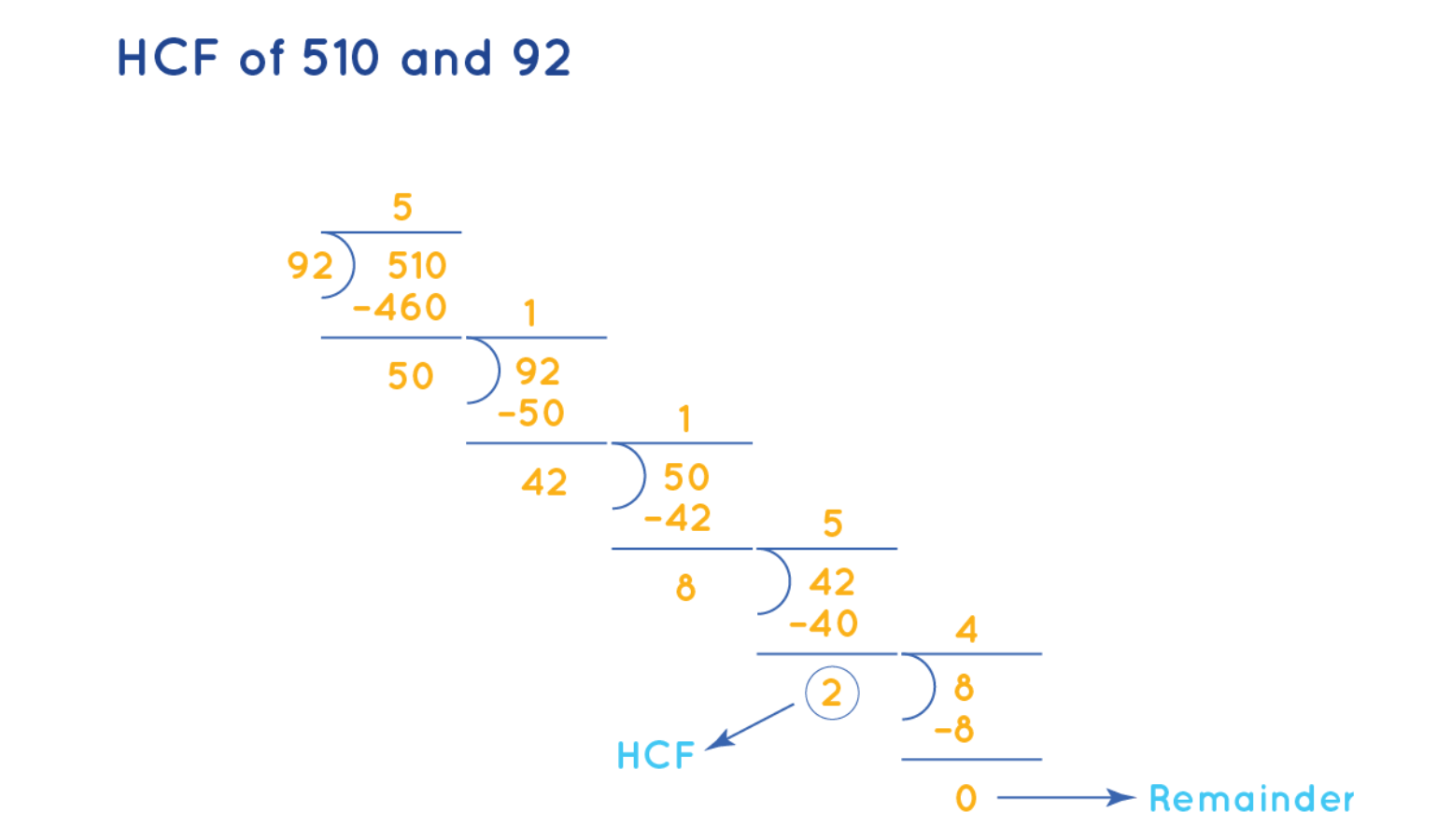
Since the remainder is 0, the divisor at this step (2) is the HCF.

LCM Calculation

The LCM is the smallest number that is a multiple of both 510 and 92. Using the relationship between HCF and LCM:

• HCF × LCM = Product of the numbers

• 2×LCM=510×92

• 510×92=46920

• LCM=46920/2=23460

Alternatively, using prime factorization:

• Prime factors: 2 (highest power 2222 from 92), 3 (from 510), 5 (from 510), 17 (from 510), 23 (from 92)

• LCM=22×3×5×17×23=4×3×5×17×23

• 4×3=12

• 12×5=60

• 60×17=1020

• 1020×23=23460

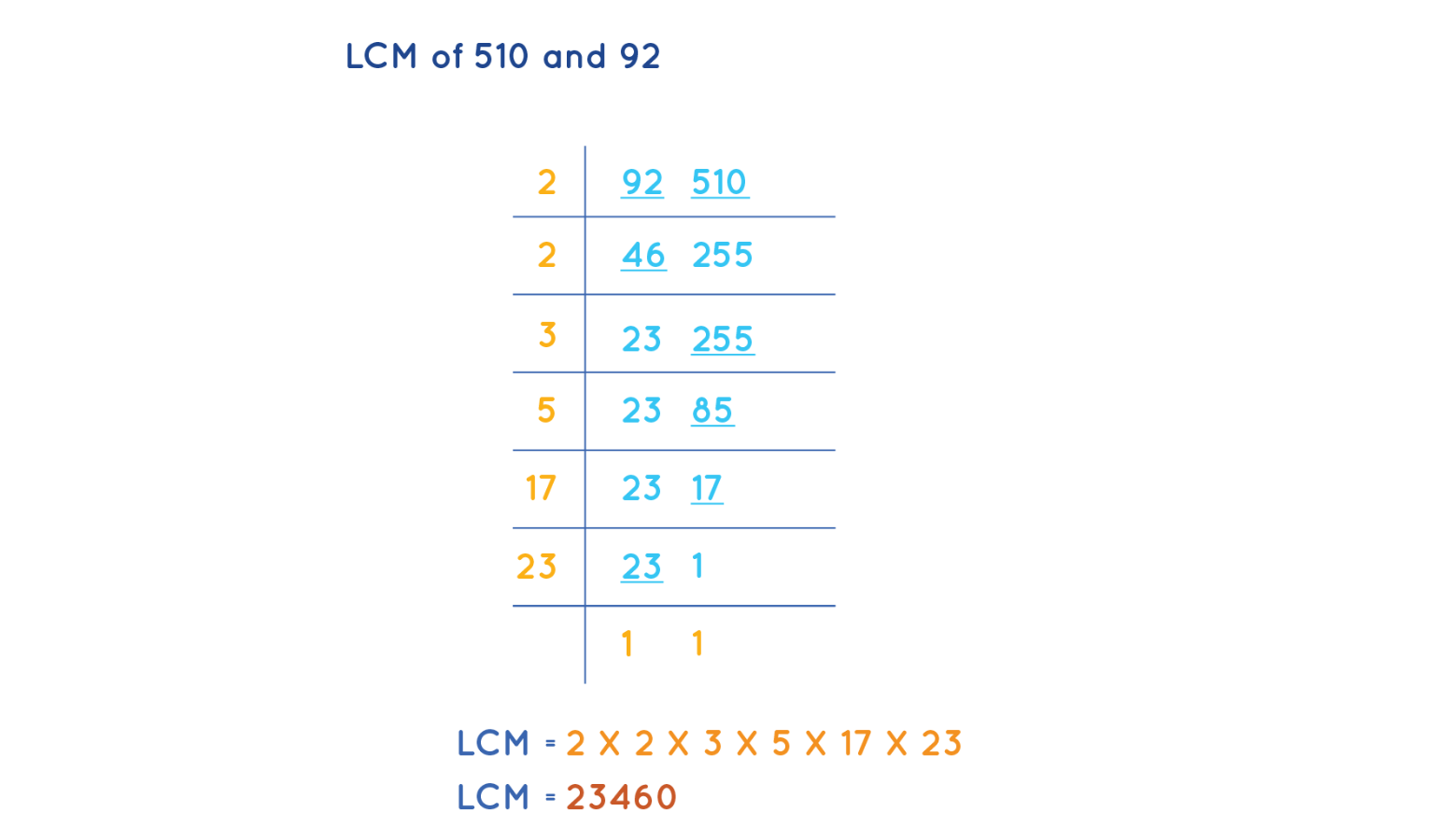
Thus, the LCM is 23460.

Final Answer

The Highest Common Factor (HCF) of 510 and 92 is 2.

The Least Common Factor(LCM) of 510 and 92 is 23460.

prime factorization of 510 and 92

lcm and hcf of 510 and 92

factors of 510